kda-tools at crates.io, or github.com/jodavaho/kda-tools view full post
I play hunt showdown a lot. It’s very fun. It’s also insanely frustrating sometimes. The game has long matches, very frantic, quick battles, and a wide variety of meaningful character specialization and equipment options. It can take dozens of matches to determine if a loadout is worth it, and there are many loadouts, and a match takes an hour … In short, it is very hard to get feedback on what equipment loadouts, tactics, or friends are useful.
Furthermore, it’s hard to know if you’re doing well lately or doing better with this loadout or just play worse with your friend Justin. Luckily, I was once paid to solve these problems for real, so let’s solve them for fun.
This is the first of likely a bunch of posts on: designing a logging system (pen and paper), defining a math problem that will help us answer general questions, then writing some Rust to solve it. (Rust is not important here, it’s just what I play with when I’m making CLI tools). This is also my first longer-form post, and my first real entry in a series, so I’m going to have to come back and re-edit this until I get my writing habits in order. Finally, I am way behind on my actual writing, so this became a procrastination mechanism. But for now, caveat emptor and enjoy!
Skip to:
or just go see the final product
But first, if you appreciate this kind of content or would like to see me take on something else, let me know! You can reach me at hello@jodavaho.io.
Step 1 Get the data
The first step in any statistical analysis program is data gathering! Unfortunately, Hunt Showdown does not support a vibrant modding community, and uses encrypted telemetry, and so rather than get super technogeek here, we’ll just write down a few key stats for each game. This is ok, there are not many, and they are all available on the summary screen at the end of a match.
What we want to be able to do is say “Every time this happened, what seemed to happen a lot as well?”. For example “Every time I carried this gun, did I get more kills?” Or, “When I play with Justin, do we kill more bosses?”
So you have to actually write down everything you want to measure.
I kept a log on paper, writing down the date, the match number and the following things:
- Kills
- Deaths
- Assists
- Bosses killed
- Bounties extracted
- Main weapon (what weapon did I bring in)
- Secondary weapon (what secondary)
I’d be suprised if it Itook me 30s to scribble this down. Later I kept a text editor open, alt-tabbed, and recorded one match per line as:
2021-10-11 k:3 d:1 b:2 a
2021-10-11 d
You can see a clear date, three kills, 1 death, two bounties extracted, and an assist. What a game! Then, of course, an immediate wipe. Hunt giveth, hunt taketh away.
By the way, this format is something I call “key value counts”1. You can define any format you want, as long as you write a parser.
We should also record “loadouts”. I did often recorded actual weapons, or just
“types”. For simplicity let’s assume I named a few loadouts that worked well
together, like sniper, shotgun, rifle, carbine etc. So the log should
look like:
2021-10-11 k:3 d:1 b:2 a sniper
2021-10-11 d shotgun
Later, I got curious about some additional “meta stats”. You can record these too! You’ll be able to correlate any variable later.
- Ambushes (how many times did we set up a fight on an unaware opponent because we knew where they were going)
- Raids (how many times did we rush an established defender, even if they were under attack already)
- Defends (how many times did we fight off attackers while defending a bounty)
- Wipes (how many times did we wipe another team)
- Loss (how many times were we wiped)
- Who I played with

A hunt-showdown actuary, maybe analyzing raid data? (credit: Midjourney)
Step 2: Form the problem
This is a classic treatment effect calculation. We want to know if a treatment (“Carry this gun instead of any other”) has an effect (“KDA rises or more bosses killed”).
So how do we model this? The punchline is I chose to assume that kills, deaths, bounties, etc, accumulated over time, were Poisson Processes2.
That is, we assume that in the K-D-A-B space of all games, the number of kills, deaths, assists, and bounties per game, were essentially Poisson Random Variables3. The KDAB values are assumed independent of eachother, but not independnet of other variables like loadout.
Poisson Random Variables
Poisson Random Variables have a single parameter of interest, $\lambda$. That $\lambda$ is basically the expected number of times the “event” (like kills) should occur each “round”. Given a $\lambda$ you can calculate a distribution of possible event counts, each with a likelihood, for a given round. That just means we can plot how likely 3 kills was given we have an average number of kills per round of 2. We can also calculate how likeley getting more than 3 kills was, given we usually get 2.
If you average two kills per game, here’s the distribution of kills you’d usually see:
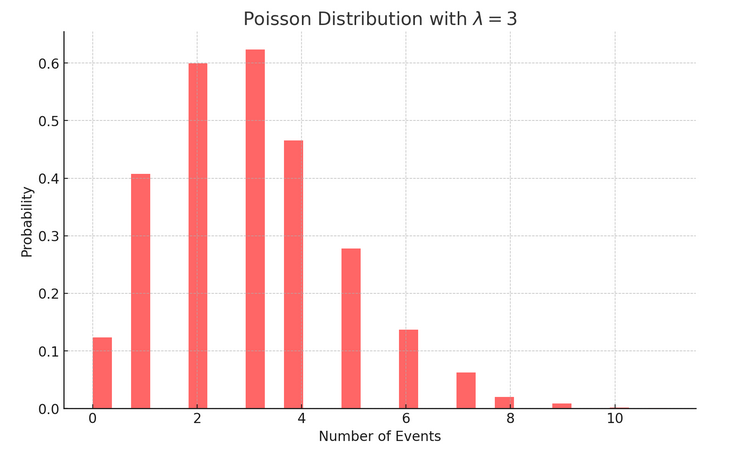
Poisson Distribution: Probability of seeing x events, given you usually see $\lambda=3$ events per round
Poisson Distribution: Probability of seeing x events, given you average $\lambda=1.2$ events per round
How can we use that? Well, we can slice the data! Suppose you wanted to compare
kills when you use sniper. You can calculate the value of
$\lambda$ given all the games with sniper ($\lambda_\text{sniper}$), versus
the $\lambda$ for all games overall, and then ask “are these equal”? Since
the best estimate of $\lambda$ for a given distribution is just the average
rate observed, we have …
$$ \begin{aligned} \lambda_\text{sniper} &= \frac{\text{sum of all kills during sniper matches}}{\text{number of sniper matches}} \\ \lambda_\text{all} &= \frac{\text{sum of all kills during all }}{\text{number of matches}} \\ \end{aligned} $$
We’d like to test
$$ \begin{equation} \lambda_\text{sniper} \stackrel{?}{>} \lambda_\text{all} \tag{1} \label{test} \end{equation} $$
You could just compare them. Of course, this is not enough to say whether they are unequal4. Random variables are usually unequal by virtue of being random. What we want to know is, are they unequal more than would be expected? That is, “do we believe the choice of loadout was a differentiating factor on K, D, A, or B values”.
Poisson Statistical Tests
Let’s recall some statistics. We can transform Eq \eqref{test} to
$$ \begin{equation} \frac{\lambda_\text{sniper}}{ \lambda_\text{all} } \stackrel{?}{>} 1 \tag{2} \label{ratiotest} \end{equation} $$
This could be a “simple-simple likelihood ratio test”5, meaning that the distribution is known for both cases, and we want to know if the $\lambda$ parameter of the distributions are the same or not. We assume they are, and want to see if we have sufficient difference to determine that was a bad assumption.
It is extremely common to do the following, given a test like Eq \eqref{ratiotest}.
- Assume they are equal (defined as the “null hypothesis”)
- Contort the equations until they are combined into a ’test statistic'
- Show that your ’test statistic’ has a nice distribution, which you can analytically bound by a value $p$.
- Calculate when your ’test statistic’ is ‘out of bounds’, i.e., your “$p$ value” is too small, meaning you’ve observed something likely unexplained by the null hypothesis.
While the definition given in the prior paragraph appeared in 1933, it is suprisingly hard to find well-explained test statistics in literature for this type of test.6. But, some suprisingly recent results were helpful. Following [Gu2008] and [Ng2005] , we find a bunch of ways of doing steps 1-4 for Poisson ratios.7, and I just chose Section 2.4 in Gu’s paper, which is a bit of lovely prose that looks like:

lovely…
Sidebar: Future work on KDA experiment design
My absolutely favorite sub-subject in statistics is Experiment Design. I wrote a whole thesis on it. Experiment design is concerned with the question: “How many measurements should I make to ensure that the statistical test will pass if there is an effect?” This is of critical importance for budgetting trials, but also for bounding the time required to track targets using robots.
For this project, I will eventually sit down an add code that will tell you how many more games you should play to determine if the loadout is useful. [Ng2005] has these values in closed form for some test statistics we could be using here.
But for now, time to write some code.

A hunter unlocking the magic of mathematics. Credit: Midjourney
Step 3 Make the program
I am using the rust programming language. Rust is great. It’s like C, which I love, but also comes with a ton of modern niceties. I hate most of what people make for Rust (i.e., bloated libraries), but that’s not the language’s fault.
As much as I’d love to walk through the detailed programming, it’s just too
much for one post. But I can present the high level steps and libraries used,
and hope to write more on this later. The code is available online8, and
is easily installed with cargo install kda-tools or by installing using
dpkg as noted in docs.
First, we want code to read the game journal, above. If you don’t have one, here’s a sample journal from my actual play history.
2021-03-12 BAR+Scope pistol K K B alone
2021-03-12 BAR+Scope pistol K D D jb
2021-03-12 Short-Rifle Short-Shotgun K D jb
2021-03-12 BAR+Scope pistol D jp+jb
2021-03-13 BAR+Scope pistol jp D
2021-03-13 BAR+Scope pistol jp B D D A A
2021-03-13 Shotgun pistol jp D
2021-03-13 BAR+Scope pistol jp K
2021-03-14 Short-Rifle akimbo alone
2021-03-17 LAR Sil pistol alone
2021-03-17 pistol-stock akimbo alone
2021-03-17 Short-Shotgun pistol-stock alone
As mentioned, this is KVC9 format. So cargo add kvc. The
documentation10 contains a simple function read_kvc_line_default which
returns a vector of keys and counts as tuples. So you only need to read each
line, parse, and we have our data!
To conduct a test, you want to go over the data, add up all rows with the factor of interest, and then using all rows as baseline. Then, calculate $\lambda_\text{h1}$ for the interesting ones, and calculate $\lambda_\text{h0}$ as the “null” hypothesis using all data, and plug into the above equation. Let’s do that for the practice data.11
The “baseline” kills / match for the practice data above is a total of 5 Kills (sumH0=5) in 12 matches (nH0=12), for a value of $\lambda_\text{h0}=5/12$.
Suppose we want to test “BAR+Scope” gives more kills than usual.
Partitioning the data, we see:
2021-03-12 BAR+Scope pistol K K B alone
2021-03-12 BAR+Scope pistol K D D jb
2021-03-12 BAR+Scope pistol D jp+jb
2021-03-13 BAR+Scope pistol jp D
2021-03-13 BAR+Scope pistol jp B D D A A
2021-03-13 BAR+Scope pistol jp K
For a total of 4 kills (sumH1=4) in 6 matches (nH1=6). ($\lambda=2/3$)
We now need to plug these into the equations above. Luckily, there’s also code for that12, which provides the function two_tailed_rates_equal, the example13 is straightforward.
let p = two_tailed_rates_equal(sumH1, nH1, sumH0, nH0);
//or
let p = two_tailed_rates_equal(4, 6, 5, 12);
In this case we get a conclusive answer, which is p=0.05! This tells use the
probability of observing $\lambda=4/6$ given my usual playing record of 5 kills
every 12 matches is very low. Meaning, something had a measureable effect!
The code is relatively straightfoward, but only if you closely follow the paper14
You can reproduce these steps with:
$ cat test | kda-explore 'K: BAR+Scope'
Processed. Read: 12 rows and 18 variables
Varibables found:
Date K alone pistol BAR+Scope B D jb Short-Rifle Short-Shotgun jp+jb jp A Shotgun akimbo LAR Sil pistol-stock
Debug: processing: K: BAR+Scope
met grp n M rate ~n ~M ~rate p notes
K BAR+Scope 4 6 0.67 1 6 0.17 0.05
Notice how we had to tell it K: BAR+Scope which means “Test kills / match
using BAR+Scope vs normal performance”.
Now, there’s no reason you would necessarily have to prompt the user for “What would you like to know”. Given we just have to add up some variables and plug into an equation, we can do this really fast so why not just test everything?
That’s what I ended up doing. The program kda-explore will output the following on this journal:
$ cat journal | kda-explore
Processed. Read: 12 rows and 18 variables
Varibables found:
Date B alone K BAR+Scope pistol jb D Short-Rifle Short-Shotgun jp+jb jp A Shotgun akimbo LAR Sil pistol-stock
Debug: processing: K D A : all
No matches found without grouping 'K', this test is useless. Skipping!
met grp n M rate ~n ~M ~rate p notes
K BAR+Scope 4 6 0.67 1 6 0.17 0.05
K jb 2 2 1.00 3 10 0.30 0.08
K B 2 2 1.00 3 10 0.30 0.08
K pistol 4 8 0.50 1 4 0.25 0.35
K Short-Shotgun 1 2 0.50 4 10 0.40 0.78
K Short-Rifle 1 2 0.50 4 10 0.40 0.78
K alone 2 5 0.40 3 7 0.43 0.91
K pistol-stock 0 2 0.00 5 10 0.50 0.74
K akimbo 0 2 0.00 5 10 0.50 0.74
K Sil 0 1 0.00 5 11 0.45 0.73
K LAR 0 1 0.00 5 11 0.45 0.73
K Shotgun 0 1 0.00 5 11 0.45 0.73
K A 0 1 0.00 5 11 0.45 0.73
K jp+jb 0 1 0.00 5 11 0.45 0.73
K D 2 6 0.33 3 6 0.50 0.53
K jp 1 4 0.25 4 8 0.50 0.35
No matches found without grouping 'D', this test is useless. Skipping!
met grp n M rate ~n ~M ~rate p notes
D BAR+Scope 6 6 1.00 2 6 0.33 0.04
D jb 3 2 1.50 5 10 0.50 0.05
D A 2 1 2.00 6 11 0.55 0.05
D pistol 7 8 0.88 1 4 0.25 0.05
D jp 4 4 1.00 4 8 0.50 0.17
D B 2 2 1.00 6 10 0.60 0.40
D Shotgun 1 1 1.00 7 11 0.64 0.57
D jp+jb 1 1 1.00 7 11 0.64 0.57
D K 3 4 0.75 5 8 0.62 0.73
D Sil 0 1 0.00 8 11 0.73 0.97
D LAR 0 1 0.00 8 11 0.73 0.97
D Short-Shotgun 1 2 0.50 7 10 0.70 0.64
D Short-Rifle 1 2 0.50 7 10 0.70 0.64
D pistol-stock 0 2 0.00 8 10 0.80 0.40
D akimbo 0 2 0.00 8 10 0.80 0.40
D alone 0 5 0.00 8 7 1.14 0.01
No matches found without grouping 'B', this test is useless. Skipping!
No matches found without grouping 'BAR+Scope', this test is useless. Skipping!
No matches found without grouping 'pistol', this test is useless. Skipping!
No matches found without grouping 'D', this test is useless. Skipping!
No matches found without grouping 'jp', this test is useless. Skipping!
No matches found without grouping 'A', this test is useless. Skipping!
met grp n M rate ~n ~M ~rate p notes
A K 0 4 0.00 2 8 0.25 0.74
A pistol-stock 0 2 0.00 2 10 0.20 0.66
A akimbo 0 2 0.00 2 10 0.20 0.66
A Short-Shotgun 0 2 0.00 2 10 0.20 0.66
A Short-Rifle 0 2 0.00 2 10 0.20 0.66
A jb 0 2 0.00 2 10 0.20 0.66
A alone 0 5 0.00 2 7 0.29 0.48
A Sil 0 1 0.00 2 11 0.18 0.33
A LAR 0 1 0.00 2 11 0.18 0.33
A Shotgun 0 1 0.00 2 11 0.18 0.33
A jp+jb 0 1 0.00 2 11 0.18 0.33
You can see it complains “This test is useless”, when it cannot find that an event had occured. This is a corner case in how the test statistic is calculated. To get around that, and allow arbitrary tests, we can use other more modern (e.g., computationally painful) methods. That’s another one for next time.
Final Product
Let’s recap. First, you need to keep a journal of matches. Then, you can either calculate the $\lambda$ values from that journal, or write some tools to do it for you. If you’d like to use my tools, they are here: (see github.com/jodavaho/kda-tools )
kda-summarywill summarize your K, D, and A values (and the usual KDA metric) over the entire journal.kda-comparewill run will look at the whole dataset and tell you if you’re doing significantly differently with different loadouts.kda-explorewill allow you to look at the conditional distributions of anything with and without anything else.
Get for debian / WSL
If you have cargo (apt install cargo), then cargo install kda-tools.
Otherwise, just grab one of the test debs in releases/ For example 1.3.0
Then, in bash/cli or wsl,
sudo dpkg -i kda-tools_1.3.0_amd64.deb
Conclusion
I’ve talked about how we can model Hunt Showdown statistics as Poisson Random Variables, how we can formulate a test to see how well we do with certain loadouts, and provided links to code which allows you to automated those tests.
I will, in the future, write up more on these tools, including discussing how non-analytical results are possible, how we can measure more than just Kills or Bounties (e.g., KDA), and how we can automate the whole thing. I’ll also dive into the code more, to provide examples of how it works.
Next, we’ll go over a more powerful tool kda-compare, which does automated testing of more than just things you can count. For example, it’ll measure “KDA” (i.e., $\frac{K+A}{D}$) and “Bounties per death” $\frac{B}{D}$, which existing analytical methods cannot do (to the best of my knowledge).
$ <journal.txt kda-compare
Processed. Read: 5 rows and 8 variables
[====================================================] 100.00 % 2696.14/s
met grp n/d val N n/d ~val M p
kda Sniper 5/1 5.00 3 2/2 1.00 2 0.06
kda JP 2/0 inf 1 5/3 1.67 4 0.49
kda Shotgun 2/2 1.00 2 5/1 5.00 3 0.77
kda JB 2/2 1.00 2 5/1 5.00 3 0.78
b/d Sniper 1/1 1.00 3 1/2 0.50 2 0.24
b/d Shotgun 1/2 0.50 2 1/1 1.00 3 0.69
b/d JB 2/2 1.00 2 0/1 0.00 3 NaN
b/d JP 0/0 NaN 1 2/3 0.67 4 NaN
Just a teaser: The first row is met grp ...
These are
- the metric name (e.g., kda or bounties / death b/d)
- item group (grp)
- value counts (n)
- deaths (d)
- the value of the metric ‘val’ with the grp
- number of matches where ‘grp’ was used (N)
- value counts without the grp (n)
- death counts without the grp (d)
- the value of the metric ‘val’ without the grp
- number of matches without the grp (M)
- and the probability that we’d randomly see that ‘val’ given the distribution of the metric without the grp.
References
Ng2005 Ng, Hon Keung Tony, and Man‐Lai Tang. “Testing the equality of two Poisson means using the rate ratio.” Statistics in medicine 24, no. 6 (2005): 955-965.
Ractliffe1964 : Ractliffe, J. F. “The significance of the difference between two Poisson variables: an experimental investigation.” Applied Statistics (1964): 84-86.
Gu2008 : Gu, Kangxia, Hon Keung Tony Ng, Man Lai Tang, and William R. Schucany. “Testing the ratio of two poisson rates.” Biometrical Journal: Journal of Mathematical Methods in Biosciences 50, no. 2 (2008): 283-298.
-
See github.com/jodavaho/kvc for more information on key-value-counts ↩︎
-
Poisson Process: https://en.wikipedia.org/wiki/Poisson_point_process ↩︎
-
Poisson random varaibles: https://en.wikipedia.org/wiki/Poisson_distribution ↩︎
-
For example, getting 1, 2, 2 kills with shotgun (avg: 5/6) vs 2, 2, 2 kills with snipers (avg: 6/6) is different, but not different enough to care about. ↩︎
-
Likelihood Ratio Test: https://en.wikipedia.org/wiki/Likelihood-ratio_test# ↩︎
-
maybe a better statistician could have derived them? ↩︎
-
I really should have followed [Ng2005] , but live and learn ↩︎
-
github.com/jodavaho/kda-tools or
cargo install kda-toolswhich pulls crates.io/crates/kda-tools ↩︎ -
The use of $H0$ to represent the null hypothesis and $H1$ to represent the “stuff that may have changed things” is mostly historical. ↩︎
-
See
one_tailedcode on poisson_rate_test/lib.rs lines 190-250 ↩︎
Comments
I have not configured comments for this site yet as there doesn't seem to be any good, free solutions. Please feel free to email, or reach out on social media if you have any thoughts or questions. I'd love to hear from you!