[Jodavaho.io]

OK, let’s talk about my diet.

I’ve started a diet, with the goal of losing 32 lbs, or ~15% of my bodyweight, to get back to my circa 2000-2005 weight. I’m happy if I achieve 80% of that loss, ending up under 200. This is a long post, in which I describe the plan, and some misunderstandings I had about dieting and weight loss.

Along the way, I built an estimator that uses data to determine my real calorie intake, needs, and activity level. The results, for me, were surprising.

In practice, the hardest part about calorie deficits is tracking calories. Burying the lede a little, it turns out LLM / ChatGPT-4 is fantastic at counting calories for you from pictures, descriptions, or rough notes.

I’ll cover all that.

What’s a diet

My definition of diet is extended calorie deficit for the purposes of losing bodyfat. I do not differentiate types of food, but I prefer high protein for appetite control. I also don’t do time-based restriction, though I find that skipping breakfast and not eating after dinner is sustainable, and that’s roughly an 18/6.

From the first two parts of this series, we have a few equations to work with: , we have a few equations to work with:

1. Mifflin-St Jeor¹ equation for Basal Metabolic Rate (BMR) is $ 10 \times weight(kg) + 6.25 \times height(cm) - 5 \times age(y) + G$, where $G$ is 5 for men, and -161 for women.
2. Total Daily Energy Expenditure (TDEE) is $BMR \times L$, where $L$ is a multiplier for your daily activity level with specific values ranging from “Sedentary” to “Extra Active”.
3. “Steady state weight” (SSW) = $\frac{1}{10}\left(cal - L \times [6.25 \times height - 5 \times age + G]\right)$
4. A weight loss model, $w(t) = SSW + (w_0 - SSW) e^{-\frac{10L}{B}(t)}$

Or, tidied up a bit:

$$ \begin{aligned} BMR =& 10 w + 6.25 H - 5A + G \\ &\text{ with } G \in \{5, -161\}\\ TDEE =&L \cdot BMR\\ &\text{ with } L \in \{1.2, 1.375, 1.55, 1.725, 1.9\}\\ SSW =& \frac{cal - L\cdot [6.25 H - 5 A + G]}{10} \\ w(t) =& SSW + (w_0 - SSW) e^{-\frac{10L}{B}(t)} \\ &\text{ with } B = 3500 | 7700 \text{ calories per unit lb|kg}\\ \end{aligned} $$

See previous posts for more details.

From this we’re accumulating python code:

from enum import Enum
import numpy as np

def bmr_m(weight, height, age):
    return 10 * weight + 6.25 * height - 5 * age + 5

def bmr_f(weight, height, age):
    return 10 * weight + 6.25 * height - 5 * age - 161

class Activity(Enum):
    SEDENTARY = 1.2
    LIGHT = 1.375
    MODERATE = 1.55
    VERY = 1.725
    EXTRA = 1.9

def calc_tdee(bmr, activity):
    """
    Calculate Total Daily Energy Expenditure
    """
    if (activity < 1.2 or activity > 1.9):
        raise ValueError("Activity must be between 1.2 and 1.9")
    return bmr * activity

def steady_state_weight(calories, activity, height, gender, age):
    """
    Reverse BMR to find weight given calories

    Accepts calories per day, activity level, height in cm, 
    gender='m'|'f', age in years

    Returns weight in kg
    """
    L = activity
    if gender=='m':
        wt = calories /  L - (6.25 * height - 5 * age + 5)
        wt = wt / 10
        return wt
    if gender == 'f':
        wt = calories /  L - (6.25 * height - 5 * age - 161)
        wt = wt / 10
        return wt
    raise ValueError('sex: m|f only')

def weight_over_time(days, calories, 
                     ht, age, gender, wt0, 
                     activity=Activity.SEDENTARY.value):
    """
    Given you want to consume `calories` per day, over the range of days, what
    will your weight be?

    Accepts wt0 in kg, ht in cm, gender='m'|'f', age in years
    Returns a list of weights over time, one per day, in kg
    """
    SSW = steady_state_weight(calories, activity, ht, gender, age)
    t = np.arange(0, days)
    exparr = np.exp(-10*activity/7700* t)
    res = SSW + exparr * (wt0-SSW)
    return res

We now have a vague sense that “in a few years” we’ll hit a steady state weight, and that we can lose weight faster or slower by choosing a different calorie intake.

We can also manually tweak the Activity enum to see how different activity levels affect our weight loss, or try different calorie intakes to try to hit a goal.

As hinted when we started, what people want is: “When will I hit my goal weight?” or “How many calories do I need to cut to hit my goal weight by a certain date?”

These are real optimization problems, and now we have the math to solve them.

Deriving calorie intake to hit a goal weight by a certain date

We derived this equation:

$$w(t) = SSW(cal,L)\cdot\left(1-e^{-\frac{10L}{B}(t)} \right)+ w_0 e^{-\frac{10L}{B}(t)} \text{} $$

Given above closed form equation, we can answer the question “If I want to lose 30 lbs by mid-summer, how many calories do I need to cut?” What we’re asking is: “Given t=days to end of diet, what is the value of calories that will result in w(t) = w_0 - <amount to lose>?”

To lose 10 kg in the next 90 days, form:

$$w_0 - 10 = SSW(x,L)\cdot\left(1-e^{-\frac{10L}{B}(90)} \right)+ w_0 e^{-\frac{10L}{B}(90)} \text{} $$

and solve for $x$.

The algorithm is essentially:

1. Solve $C_e = e^{-\frac{10L}{B}(90)}$
2. Calculate $C_p = (6.25 H - 5 A + G) / 10L$
3. Plug into $w_0 - 10 = \left(\frac{cal}{10L} - C_p\right)\cdot\left(1-C_e \right)+ w_0 C_e \text{} $
4. which reduces to $cal = 10L \left( w_0 - \frac{10}{1-C_e} + C_p\right) $

# import numpy as np # already imported above, but just remember
def predict_calories_to_lose(days, wt0, wt_target, ht, age, activity=Activity.SEDENTARY.value):
    """
    Given you want to lose `wt0 - wt_target` (kg!) in `days`, what should your
    daily calorie intake be?

    Accepts wt0 in kg, ht in cm, age in years
    Returns calories per day
    """
    C_e = np.exp(-10*activity/7700 * days)
    G = 5 # or -161 for biological females
    C_p = (6.25 * ht - 5 * age + G) / 10
    return 10 * activity * (wt0 - (wt0 - wt_target) / (1 - C_e) + C_p)

Determining arrival time at a given weight from a given strategy

You may also want to know when you’ll hit a given weight, given a strategy. This is no more difficult, we just solve for $t$ in the above equation.

$$\begin{aligned} w(t) &= SSW + (w_0 - SSW) e^{-\frac{10L}{B}(t)} &\text{} \\ w_{target} &= SSW(calories,L) + (w_0 - SSW(calories,L)) e^{-\frac{10L}{7700}(t)} &\text{} \\ w_{target} - SSW(calories,L) &= (w_0 - SSW(calories,L)) e^{-\frac{10L}{7700}(t)} &\text{} \\ \frac{w_{target} - SSW(calories,L)}{w_0 - SSW(calories,L)} &= e^{-\frac{10L}{7700}(t)} &\text{} \\ \ln\left(\frac{w_{target} - SSW(calories,L)}{w_0 - SSW(calories,L)}\right) &= -\frac{10L}{7700}(t) &\text{} \\ t &= -\frac{7700}{10L} \ln\left(\frac{w_{target} - SSW(calories,L)}{w_0 - SSW(calories,L)}\right) &\text{} \\ \end{aligned}$$

Note, the fraction $\frac{w_{target} - SSW(calories,L)}{w_0 - SSW(calories,L)}$ is the fraction of the way to the target weight, and, assuming you’re losing weight, is always less than 1. It somewhat curiously represents “target percent excess after diet” in a way.

This yields a simple algorithm:

def predict_days_to_weight(wt_target, calories, wt0, 
                           ht, gender, age, activity=Activity.SEDENTARY.value):
    """
    Given you want to hit `wt_target` (kg!) on a diet of `calories` per day and
    activity level `activity`, how many days will it take?

    Accepts wt0 in kg, ht in cm, age in years, gender='m'|'f'
    Returns days
    """
    SSW = steady_state_weight(calories, activity, ht, gender, age)
    numerator = wt_target - SSW
    denominator = wt0 - SSW
    return -7700/(10*activity) * np.log(numerator/denominator)

So there you have it! A mathy way to come up with your own activity / calorie balance that makes sense for you.

In case you’re curious I ran my situation as follows:

Start = to_kg(222)
End = to_kg(190)
Diff = End - Start
calsed = predict_calories_to_lose(158, Start, End, to_cm(77), 43, Activity.SEDENTARY.value)
calslight = predict_calories_to_lose(158, Start, End, to_cm(77), 43, Activity.LIGHT.value)
calsmod = predict_calories_to_lose(158, Start, End, to_cm(77), 43, Activity.MODERATE.value)

and got:

SED Calories to lose -32.0 lbs in 158 days: 1625.19
LIGHT Calories to lose -32.0 lbs in 158 days: 1964.75
MOD Calories to lose -32.0 lbs in 158 days: 2304.17

So, I’ve chosen 2000 as a target, revived the running and weightlifting, and I’m on my way.

In the next part, we’ll discuss how I track caloires, which is the hardest part, honestly.

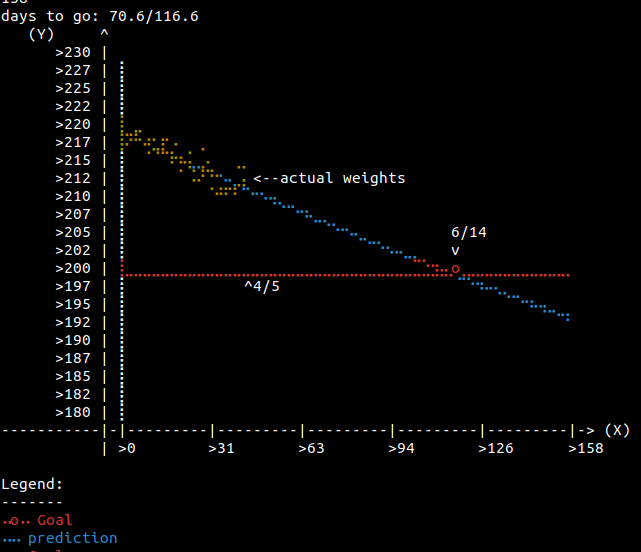
But for now, a teaser on my progress, for which the goal arrival is updated daily. We’ll talk about this in the next post.